Chapter 16 Solutions to Exercises - Circuit Analysis and Design

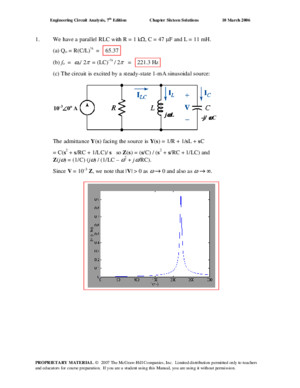
  Engineering Circuit Analysis, 7 th  Edition Chapter Sixteen Solutions 10 March 2006 1 We have a parallel RLC with R = 1 k  Ω , C = 47 μ F and L = 11 mH (a) Q o  = R(C/L) ½  = 6537 (b)  f  o  = ω  o / 2 π   = (LC) -½  / 2 π   = 2213 Hz (c) The circuit is excited by a steady-state 1-mA sinusoidal source: 10 -3   0 o  A  j    L -j/ C The admittance Y ( s ) facing the source is Y ( s ) = 1/R + 1/ s L + s C = C( s 2  + s /RC + 1/LC)/ s  so Z ( s ) = ( s /C) / ( s 2  + s /RC + 1/LC) and Z (  j ω  ) = (1/C) (  j ω  ) / (1/LC – ω  2  +  j ω  /RC) Since V  = 10 -3   Z , we note that | V | > 0 as ω    →  0 and also as ω    →   ∞ PROPRIETARY MATERIAL © 2007 The McGraw-Hill Companies, Inc Limited distribution permitted only to teachers and educators for course preparation If you are a student using this Manual, you are using it without permission  Engineering Circuit Analysis, 7 th  Edition Chapter Sixteen Solutions 10 March 2006 2 (a) R = 1000 Ω  and C = 1 μ F Q o  = R(C/L) ½  = 200 so L = C(R/ Q o ) 2  = 25 μ H (b) L = 12 fH and C = 24 nF R = Q o  (L/ C) ½  = 4472 m Ω  (c) R = 1217 k  Ω  and L = 100 pH C = (Q o  / R) 2  L = 270 aF PROPRIETARY MATERIAL © 2007 The McGraw-Hill Companies, Inc Limited distribution permitted only to teachers and educators for course preparation If you are a student using this Manual, you are using it without permission  Engineering Circuit Analysis, 7 th  Edition Chapter Sixteen Solutions 10 March 2006 3 We take the approximate expression for Q of a varactor to be Q ≈   ω  C  j R   p / (1 + ω  2  C  j2  R   p  R  s ) (a) C  j  = 377 pF, R   p  = 15 M Ω , R  s  = 28 Ω  (b) dQ/d  ω   = [(1 + ω  2  C  j2  R   p  R  s )(C  j  R   p ) - ω  C  j R   p (2 ω  C  j2  R   p  R  s )]/ (1 + ω  2  C  j2  R   p R  s ) Setting this equal to zero, we may subsequently write C  j R   p  (1 + ω  2  C  j2  R   p  R  s ) - ω  C  j R   p (2 ω  C  j2  R   p  R  s ) = 0 Or 1 – ω  2  C  j2  R   p  R  s  = 0 Thus, ω  o  = (C  j2  R   p R  s )  –½  = 1294 Mrad/s = 2100 MHz Q o  = Q( ω   = ω  o ) = 3660 PROPRIETARY MATERIAL © 2007 The McGraw-Hill Companies, Inc Limited distribution permitted only to teachers and educators for course preparation If you are a student using this Manual, you are using it without permission